Mar. 22-26

This week, I learned about the various ways ionic compounds could form.

The first type of reaction I learned about is a single replacement reaction, which forms when the single reactant swaps place with one other same kind of element (e.g. AlN + P ––––> AlP + N), hence the products are an ionic compound and an element. But, if N were not singular in the reactant, then it as a diatomic atom, can bond to itself to form N2. But, once a product, the amount of nitrogen remains the same, so 2 nitrogens.

Example of single replacement reaction

Next, I learned about double replacement reactions. These form when two double element compounds swap two elements into the other compound. This is how compounds, such as MgF2 and NaCl form. MgCl2 + NaF ––––> MgF2 + NaCl is a perfect example of this. This forms a perfect product because the two still are ionic compounds with 1) metal + nonmetal 2) Have neutral charges. Double replacement reactions are like single replacement reactions because both involve ionic compounds, and sometimes, both have diatomic elements that bond to themselves at times to balance the equation. But, the difference is that there are two ionic compounds in this reaction, not one.

Example of double replacement reaction

Then, I learned about combustion reactions, which is formed when a hydrocarbon and an oxygen always form the products of carbon dioxide and water (e.g C3H8 + O2 ––––> CO2 + H2O). Last week, I wrote that I wasn't sure as to how these combine to form CO2 and H2O. This reminds me of when I was learning about the process of photosynthesis in my Honors Biology course. All I knew was that glucose (C6H12O6) and O2 combined to form CO2 and H2O, but I wasn't sure as to what happened with the O5, the H10, and the C5. Essentially, CO2 and H2O are the products that form, but in biology, the quantity isn't labeled, which confuses many students.

Example of combustion reaction–photosynthesis

To balance any chemical equation such as this one, glucose and diatomic oxygen, you need to look at the number of carbons first. Since there are 6, you can conclude that 6 CO2 will form. In the formula glucose itself, you can see the unsimplified empirical formula of water. With H12O6 there, it can be simplified to H2O since 12:6 has a 2:1 ratio, just as hydrogen does to oxygen. Therefore, since there are 12 H and H2O results, there are 6 H2O since H2=2 hydrogen atoms combined. Hence, with 6 H2, it stays proportionate with the 12 Hydrogens in one molecule of glucose.

But, to balance the reactants, look at the products. Since there are 6 O atoms in 6 H2O and 12 O atoms in 6 CO2, there is a total of 9 O2 since 6 O atoms in water is equivalent to 3 O2. So, to balance glucose and diatomic oxygen, there is 1 C6H12O6 and 6 O2 since the 1 O6 is equivalent to 3 O2.

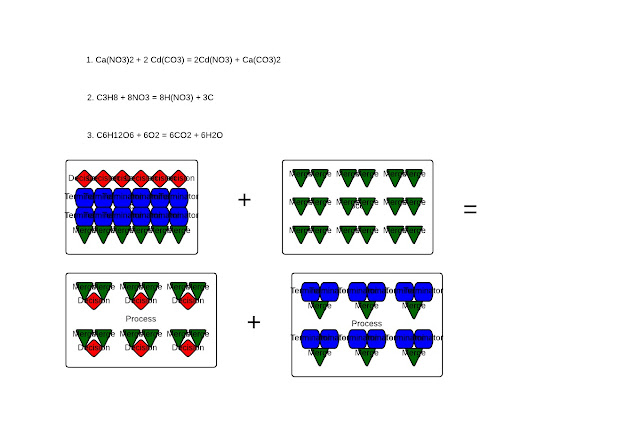Showing balanced equations and a particle diagram of photosynthesis

Using this same process, you can conclude that with C3H8 + O2 forming H2O and CO2, the products are 3 CO2 and 4 H2O. Hence, the reactants are 1 C3H8 and 5 O2.

Example of synthesis reaction

Lastly, I learned about Synthesis and Decomposition. Synthesis forms when two diatomic reactants combine to form a single product (e.g. Na + I2 ––––> NaI). Decomposition, on the other hand, is the inverted process of this. The single reactant chemically separates (decomposes) into two elements, whether one of them is diatomic or not (e.g. Na2(CO3) + 2HCl ––––> 2NaCl + H2(CO3)).

But, what does it mean to have 2 Li2(SO4) and 1 Al(PO4)? It means the ratio of the amount of each compound to the other in terms of moles. So, in other words, 2 LiNa means 2 moles of {Li and SO4} because 2[Li(SO4)] means 2Li and (SO4)2, and 1 Al(PO4) means 1 mole of {Al and PO4}. Hence, these moles have a 2:1 ratio.

Example of decomposition reaction

In order to find their molar masses, one must find the molar masses of each element first, then look at the number before the compound to determine the number of moles, and to add the numbers together. But, before the molar masses of each element are listed, let's consider a very important rule: whatever the number of moles, ignore for now so you don't screw up your math. Once it's calculated, multiply by number before the compound.

For Li2(SO4), the molar mass of Li is 6.94, the molar mass of S is 32.07, and the molar mass of O is 16. But, to represent how they combined together, let's consider the number of the elements. Since Li2 is 2*{6.94 g/mole} + Sulfur + {32.07g/mole}+ 4 O *{16g/mole} form 109.95g/mole, we can conclude that the total molar mass of 2Li(SO4) is 219.9g.

But, what if you wanted to find the number of particles this compound has? To do so, find the molar mass first. In this case, we did, so we can multiply that by the number of particles for every mole, which is 6.02*10^23. Hence, the number of particles total is 1.32*10^26 particles.

Mar 15-19

This week, I reviewed over binary and ternary ionic compounds, transition metals, molecular compounds, and acids. These were the topics I identified, defined, and charted in an Infographic I made on Lucidchart, which can be used through the Google Drive to make and store charts, graphs, and infographics.

The assignment on Monday was to define each of the following above and define how to find the chemical formulas of each. To make this, dragged the flowchart boxes onto the page from the menu on the left side. To type in information, click the Text icon and click in the box. This will frame the textbox, where you can type anything in. To resize the items, click on one of the diagonal corners and drag.


The neat thing about Lucidchart is that you don't have to worry about proportion size because it has a lock feature, which keeps the object in proportional size.

These are the things I learned as I made went along. I've never used Lucidchart before, but because of my tech curiosity and Mr. Abud's recommendation, I tried it out.

However, since I couldn't use this in class due to slow Internet connection, I used it on an up-to-date MacBook, which has great Intel and Internet connection, at home.

The picture shows the menu options from top to bottom:
1) Text and standard boxes
2) Flowcharts
3) Containers
4) Shapes
5) Upload Image

To make the infographic, I creatively chose different colors for the divisions of ionic compounds, then molecular compounds, acids, etc. I then used differently-shaped boxes to list examples of different compounds. I used relevant pictures for each of the chemical compounds and placed them underneath the charts, but I had to drag the pictures onto my desktop first and then upload them onto Lucidchart.

In the boxes, I defined binary compounds as simply a metal and a nonmetal chemically combining due to opposite charges and attractions. I then chose NaCl as one and said that to write the formulas of binary compounds, the charges must add up to zero because ionic compounds form neutral charges, and if a compound had a positive charge and a negative charge that wasn't the opposite of the positive charge (e.g. -2 and 1), then you multiply the lesser charges, or both if necessary, by the least common multiple. This, I noticed, was the same way to write the formulas with ternary compounds. Ternary compounds are formed when a polyatomic ion and a metal element (sometimes a transition metal) chemically combine due to ionic charges. An example of a ternary compound is Na(NO3). An example of a ternary compound with a transition metal is Cu III PO4 because copper, a positively charged transition metal, can change its charge depending on the negatively charged nonmetal. Hence, as PO4 loses three electrons to neutralize its own charge, it simultaneously neutralizes copper's charge by making it less positive.

I also then defined a molecular compound, which I said was formed when nonmetal elements combine due to covalent bonding (sharing of electrons). Based on the number of electrons shared, this defines their negative charge (e.g. NO3 has -1 charge because nitrogen has one less negatively-charged electron than oxygen, hence the charge is -1).

Lastly, I mentioned acids, which I said could be formed as long as hydrogen was written first in the formula and made the charges of the compound neutral (e.g. acetate acid is neutral because the C2H2O3 gives one electron to the hydrogen, hence making acetate more positive and the hydrogen less positive.) But, either way, acids are like ionic compounds because they both have neutral charges.

To convey this information, I linked arrows to the boxes to whatever boxes pertained to those boxes. But, this seems confusing alone without any sort of way to differentiate the information, which is why I used different colors. I colored the boxes pertaining to ionic compounds in general yellow, binary compounds green, ternary compounds blue, transition metal ternary compounds light teal, acids grey, and molecular compounds peach.

In case I missed any information or left a few things vague, I made a list of the rules for writing chemical formulas for ionic and molecular compounds on the side.

These icons are ways to organize information.

Once I completed my infographic and shared via Twitter and Google Drive, I also wrote a blog reflection. I think that writing blog reflections is a good way to look at how other people organize the information they think is important to discuss. However, since I am a perfectionist, I also find one of the cons of reading other blogs to be that some don't put in the effort, some leave gaps in information, or some blog posts have not been posted. But, by looking at both the pros and cons, I can fairly assess other people's blogs and grade them based on the requirements they met, or lack thereof.

However, I am also hypersensitive to criticism. Since I put in a great detail of attention to blogs and update whenever necessary, I hate it if other people rate me a 3.5, not a 4, which is the highest grade possible.

I also think that reading other blogs can be helpful if I need to study for assessments and have gaps in my knowledge on chemistry that I need to fill.

The Various Ways Chemical Compounds Form …

Lastly, I learned further about writing chemical formulas and ascertaining what compounds will form after chemical reactions. As long as one knows the types of compounds that can be formed, it comes easily–as it did for me.

Single replacement reaction

The first type of reaction I learned about is a single replacement reaction, which forms when the diatomic atoms (Bromine, Iodine, Nitrogen, Chlorine, Hydrogen, Oxygen, and Flourine) bond to themselves to form diatomic molecules (Br2, I2, etc) in order to form chemical compounds.

Next, I learned about double replacement reactions. Although this seems self-explanatory, I will explain. Think of four baskets of four fruits. Two of the baskets are in one group while the other two are in a different group. As soon as the traders decide to swap one of the baskets from each group, you get a different combination of fruits. This is how it works in order to form neutrally charged MgF2 + NaCl. MgCl2 + NaF ––––> MgF2 + NaCl is a perfect example of this. This forms a perfect product because the two still are ionic compounds wiht 1) metal + nonmetal 2) Have neutral charges. In a sense, these are like single replacement reactions because both may have diatomic elements that bond to themselves at times to balance the equation.

Then, I learned about combustion reactions, which are one of the easiest of compounds to remember because the reactants of hydrocarbon and an oxygen always form the products of carbon dioxide and water (e.g C3H8 + O2 ––––> CO2 + H2O). Although they combine to form neutrally-charged compounds, I'm not sure as to why C3H8 was combined the way it was without being neutrally charged and what happened to the remaining C2, H7, and how did the extra oxygen form from analready diatomic oxygen? Did it have to do with the fact that H2 + O2 ––––> H2O, and the extra O combined with C3H7?

Lastly, I learned about Synthesis and Decomposition. Synthesis forms when two diatomic reactants combine to form a single product (e.g. H2 + O2 ––––> H2O). Decomposition, on the other hand, is the inverted process of this. The single reactant chemically separates (decomposes) into two elements, whether one of them is diatomic or not (e.g. NaCl ––––> Na + diatomic Cl2). I, however, am not sure as to how a compound can decompose, and I want to know the chemistry behind it. I hypothesize that it may have to do with the fact that an electrical current can pass through and separate them, like when H2O ––––> H2 + O2 form during the electrolysis experiment.

Therefore, by understanding the different ways compounds form and decompose, one can get the basic understanding that this is how ionic, molecular, and acidic compounds form.

Synthesis reaction

Mar 8-12

This week, I learned about molecular compounds through the practice problems I did in class.

A molecular compound is formed when two or more nonmetal elements combine to form a compound. They attract through sharing, not transferring electrons. This then differentiates between ionic and nonionic compounds.

Ionic bonding=transferring and receiving of electrons

The differences between an ionic and a molecular compound are that an ionic is form by metal and nonmetal elements that attract to each other because of their opposite charges (+ metal and - nonmetal) and transferring of electrons to neutralize their charges. On the other hand, a molecular compound is form when the nonmetal elements play tug of war with electrons but don't transfer them. Hence, molecular compounds don't have neutral charges. They are negatively charged for the most part.

Because molecular compounds don't share electrons, I realized that they bonded in different ways. They share electrons through covalent bonding, which occurs when the negatives in atoms don't attract due to the negative nonmetal elements. Instead, they repel and reveal the positives. This then creates an overlapping area of electrons. The electrons are shared between the two atoms combined. The mobile electrons in the molecular compound rotate anywhere, but mainly near the more slightly positive atom due to a weak attraction between the electrons and the atom. But, the electrons, when they approach the other electrons, repel, due to the same negative charges.

This week, I also learned about how to combine molecular compounds and ionic compounds as well. To combine ionic compounds, the ions must neutralize in order to form an ionic compound. One of the board problems I did involved combining a "polyatomic ion" (a negatively charged conglomeration of many atoms) with a transition metal. To solve those, I knew I had to know the charge of the polyatomic ion first since the transition metal's charge varies depending on the charge of the other element. This is because an ionic bond attracts the transition metal and the nonmetal polyatomic ion together, forming a neutrally charged ionic compound.

Copper I Nitrate

For example, in Cu(NO4), the charge of copper would be +1 since the nitrate has a charge of -1. As the copper combines with the nitrate, the nitrate transfers electrons to copper, neutralizing copper and nitrate. With the needed electron in NO4, not only does the charge become neutral, but I also think that an ionic bond now holds N and O4 together, making their attraction to each other even stronger. Therefore, the new ionic compound formed is Copper (I) Nitrate. The Roman numeral indicates a transition metal's charge.

I also wondered about labeling chemical compounds if the subscript of each was a certain number. If I had to label the specific compound, what would I call it? For example, what would I call N5O2? Knowing that there are 5 nitrogen atoms and 2 oxygen atoms, this compound is called penta-nitrogen dioxide. Therefore, I learned that depending on the subscript of the elements, you use the prefix (tetra, for example, to represent four) and put it before the element. The second or last element in the compound has the suffix -ide at the end, except with hydrogen.

Covalent bonding=sharing of electrons

One of the baffling things also seemed to center around the polarity between H2O. I am not sure as to why, but oxygen has an uneven pull on the hydrogen atoms. But, how can this be when they have a neutral charge? It seems to me that polar substances only form if the compound isn't neutrally charged. Therefore, I think it's possible for molecular compounds to have polarity.

In H2O, the electrons seem to attract to one other H atom, making it more negative, and the other one more positive. Knowing that the electrons repel each other and are mobile, they can move around the more positive H atom. But, for the most part, the electrons surround the other H atom. Because of this, I wonder if this may be linked to or causes its polarity.

I also wonder if two nonmetal elements combine and have a neural charge, then would they form an ionic compound or a molecular compound. An example I can think of this is C(NO3)4 because carbon has +4 charge and (NO3)4 with a charge of -4, hence forming a neutral charge. This I seemed to struggled with because I like to think that there is always a grey area in between and that things aren't just black and white. I think C(NO4)4 is an ionic compound because carbon has a charge of +4 and NO4 has a charge of -1, so C(NO4)4, logically, would neutralize and become ionic through ionic bonding. But, then C(NO4)4 could be a molecular compound because carbon and nitrate are both nonmetals and carbon may transfer or receive electrons depending on other atoms it combines with. Finding more support for the latter choice, I think it's most likely a molecular compound since both are nonmetals.

Mar. 25-28

This week, I learned more about what when elements combine to form substances.

For the most part, the charges of the elements were consistent and unchanging. But, I realized that wasn't the case with transition metals. Transition metals, depending on the charges of the other elements they combine with to form an ionic compound, can alter its charge.

During the beginning of the lab, CuCl was an ionic compound. Cl in CuCl has a charge of -1, hence Cu must have a charge of +1.

This is what I learned in the copper chloride lab. The objective was to see what would happen if water and copper chloride chemically combined together.

I hypothesized that when they combined, the copper would stay the same since it is a metal while chlorine, hydrogen, and oxygen are gases. To combine them together, we used the electrolysis equipment. My group and I filled the trough with 100 mL of water and 4 g of copper chloride.As the copper chloride was combined with the water, the water turned blue. I concluded this was the case because the copper oxidized as the CuCl bonded with H2O.

But, if H2^2 charge + O^-2 charge + Cu^X charge + Cl^-1 charge combined, then how would they form an ionic compound? In order for the ionic compound to be neutral, the charge of copper would have to be +1. However, I noticed that at the bottom of the trough, there was oxidized copper. While the CuCl combined with water, the oxygen separated the copper while the H2 separated the chlorine. As the separation between the two occurred, the copper was oxidized by the oxygen atom in the process.

But, what would copper's charge be if it combined with oxygen? Knowing that copper is a conductive positively charged metal and knowing that oxygen has a charge of -2, copper combined with oxygen must have a charge of +2. In this case, then how would the chlorine combine with the H2O. Already knowing that H2O is an ionic compound already, it wouldn't make sense for it to combine with chlorine. Therefore, the copper and the chlorine were separated from each other as the copper chloride was combined with water.

Because the CuCl dissolved in water, I concluded that the CuCl ions became polarized, hence interrupting intermolecular forces and phase changes. If this were the case, then I wonder if factors, such as melting point and freezing point would be different from CuCl and just copper and chlorine. If this would be true, then the attraction between the particles would change. I think that as copper and chloride were separated from the water, the attraction between the CuCl ions and the H2O ions was less than that of the attraction between copper and chloride atoms.

Knowing that single elements regain their charge once separated from ionic compounds, I concluded this is what happened to chlorine and copper. Knowing that chlorine gain the electrons that copper lost, chlorine would become more positive while the copper became more negative.

This week, I also participated in the electroscope lab, which pertains to charge induction. I made my electroscope using aluminum, a glass jar, and a plastic lid taped to the glass jar. To make the electroscope, I poked a hole in the middle of the ball and stuck the rod through it so the ball wouldn't fall off of the rod. Then I poked a hole in the plastic lid and stuck the rod through the hole. Then, I bent the bottom at a 90º angle and attached the unwrinkled and even-length aluminum leaves.

Then, I tapped the rod to the plastic lid and then taped the lid on the glass charge.

To test the conductivity of my electroscope, I rubbed a balloon against my shirt to charge the balloon. As soon as I held the balloon over the aluminum ball, electrostatic electricity took place in the aluminum rod. I almost made the mistake that the electrons were being transferred from the balloon to the aluminum. But, as soon as I differentiated between that and chemically combined substances, I then realized that the polarity was only being affected, not the number of electrons between the balloon and the aluminum.

Since the aluminum itself was neutrally charged just as the balloon was, charge induction occurred. The negative charges in the aluminum were only being shifted as the balloon was brought near it. Knowing that the electrical current passed through the rod, I concluded that it must have passed through the leaves at the bottom. Since the polarity was shifted, I figured that the negatives and positives were being evenly shifted together toward the leaves.